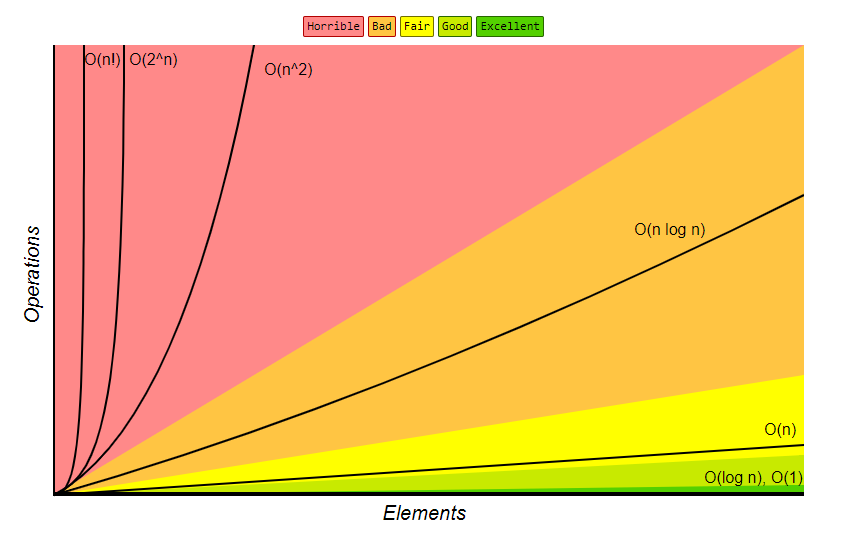
What is time complexity?
Time complexity is a measure of how the running time of an algorithm grows as the size of the input data increases.
If you ever solved competitive programming questions(usaco 💀), or just any in general, you might’ve experienced your perfectly functional code failing due to time constraints.
This also applies to real life scenarios, like ensuring user convenience on a website or in a game. Users wouldn’t want a game to take two hours to load… This is why time complexity is so important.
Big-O & other notations
Here are 3 ways of expressing time complexity:
- Best-case scenario: Big-Ω(omega)
- Average-case scenario: Big-Θ(theta)
- Worst-case scenario: Big-O
You might wonder which notation to use, but we prioritize Big-O. This is because we need to focus on the worst-case scenario in order to design systems that are the most reliable.
To be more clear, I’ll give examples for each case:
Imagine we’ve designed an algorithm that displays a best-case running time of 1 second, an average-case of 1 minute, and a worst-case of 1 hour. We will also execute the algorithm 100 consecutive times for each case explained.
Best-case scenario:

With the best-case theory, we’d expect the algorithm to take 100 seconds. But, the actual execution could easily take well over an hour if a worst-case instance occurs.
Average-case scenario:
Same applies here. We’d first expect the algorithm to take 100 minutes, then struggle with the same trouble above if the algorithm takes longer due to worst-case instances.
Worst-case scenario:
You might think that this is too extreme, but considering the worst-case would be far better than struggling with unexpected delays, as mentioned above.
This is why we primarily use the Big-O notation.
Now, let’s explore the most common time complexities, going from fastest to slowest. Also keep in mind that we will use N to represent the size of our input.
O(1): Constant

An algorithm with O(1) time complexity means that its execution time remains constant regardless of the input size (N). It performs a fixed number of operations.
public class O1Example {
public int getElement(int[] arr, int index) {
return arr[index];
}
}
int[] arr = {1, 2, 3, 4, 5};
int index = 0;
System.out.println(O1Example(arr, index));Here, accessing the first element(arr[0]) of arr takes the same amount of time, whether the array contains 5 elements or 5 gazillion.
O(log n): Logarithmic

Algorithms with O(log n) time complexity involve operations that halve the input size with each step. You can think of binary search as an example of this, as shown below.
public class OLogNExample {
public int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (arr[mid] == target) return mid;
else if (arr[mid] < target) low = mid + 1;
else high = mid - 1;
}
return -1;
}
}As you might now, in a binary search, the portion of the array that needs to be searched is cut in half with each comparison.
O(n): Linear
Algorithms with O(n) time complexity mean that their execution time grows linearly with the input size. So, if the input doubles, the time taken doubles.

public class ONExample {
public void doSomethingLinear(int n) {
for (int i = 0; i < n; i++) {
// do something for 1 second
}
}
// This is still O(n) as constants are dropped
public void doSomethingLinearWithCoefficient(int n) {
for (int i = 0; i < 2 * n; i++) { // Ex) 2n operations
// do something for 1 second
}
}
}Function doSomethingLinear seems like as n increments, the execution time increments at the same pace. Exact example of O(n).
But for the function doSomethingLinearWithCoefficient, you might think that its complexity is O(2n). Because as n increases, the execution time also appears to double, right? WRONG. Big no.
One thing to keep in mind when analyzing time complexity is that we focus on the dominant term and ignore constant coefficients. This is because, as input size (N) grows very large, the highest power of N in the expression will completely dominate the growth rate of the algorithm.
For example, in an expression like N² + 5N + 100, as N approaches infinity, the N² term will grow much larger than 5N or the constant 100.
Same applies for O(n²) below.
O(n²): Quadratic

Algorithms with O(n²) time complexity mean that their execution time grows quadratically with the input size. This most commonly occurs when you have nested loops where there are for loops in one another.
public class ON2Example {
public void doSomethingQuadratic(int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
// do something for 1 second
}
}
}
// Still O(n²) as constants are dropped
public void doSomethingCubic(int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) { // Ex) n^3 operations
// do something for 1 second
}
}
}
}
}O(2^n): Exponential

One of the slowest big-O notations. You might want to consider rewriting your code if yours look like this. 💀
Anyways, algorithms with O(2^n) time complexity mean their execution time doubles with each addition to the input size. This is often seen in brute-force solutions that explore all possible subsets or combinations. One famous example of this is the recursive Fibonacci sequence, as shown below.
public class O2NExample {
public long fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
}Comparably moderate increases of the input size might lead to impossible execution times.
What is space complexity?
Just as time complexity measures how long an algorithm takes, space complexity measures the amount of memory (space) an algorithm needs to run as the input size increases.
Similar to time complexity, space complexity is also expressed through the big-O notation.
O(n) in space complexity
Here’s a function that takes an array of integers and returns a new array containing the squares of each number:
public class ArrayOperations {
public int[] squareElements(int[] originalArray) {
int[] squaredArray = new int[originalArray.length];
for (int i = 0; i < originalArray.length; i++) {
squaredArray[i] = originalArray[i] * originalArray[i];
}
return squaredArray;
}
}In this function, squaredArray changes directly proportional to the length of originalArray. This means that if originalArray has n elements, the squaredArray will also have n elements, thereby requiring O(n) space.
Is it important tho? 😤
Not as important as time complexity. Space complexity is still important, especially in specific scenarios.
It was much more important a couple of decades ago, such as when developers of super mario had to shove their game into a 40KB file. Now, many modern computing environments have abundant memory, so space complexity might not seem that important.

Still, when dealing with devices with limited memory or massive datasets, space complexity should still be considered.
Conclusion is that you, yes YOU who didn’t even pass USACO bronze(me😭), should just focus on improving your code’s execution time.
Random

Also, if you like pokemon, try thinking of time complexity as Dialga and space complexity as Palkia(respectively being the god of time and god of space). Really helps you remember stuff.
Leave a Reply